Optimizasyon, hemen hemen tüm mühendislik çalışmalarında karşımıza çıkan bir en iyileme çalışmasıdır. Görüntü işleme ve bilgisayarlı görü alanında, özellikle Makine Öğrenmesi ve Örüntü Tanıma alanlarında önerilen Doğrusal Regresyon, Lojistik Regresyon Analizi, Destek Vektör Makineleri gibi pek çok algoritmanın matematiksel denklemlerinin çözümü için kullanılmaktadır. Bu yazımızda literatürde sıklıkla kullanılan gradyan tabanlı optimizasyon algoritmaları üzerinde durulacak, bu algoritmların teorik çalışması incelendikten sonra, algoritmaların artı ve eksi yönleri örnek bir problem üzerinden anlatılacaktır.

Elimizde

\[\min_{\mathbf{x} \in \mathbb{R}^n} f(\mathbf{x})\]

şeklinde verilen bir koşulsuz en iyileme problemi olduğunu varsayalım. Burada $f$, $\mathbb{R}^n$ uzayında sürekli türevlenebilir bir fonksiyon ise, en iyileme probleminin çözümü $\nabla f(\mathbf{x}^k) = 0$ çözümünü sağlayan tüm $\mathbf{x}^1, \mathbf{x}^2, \dots, \mathbf{x}^m$ noktalarından $\min_{k=1,\dots,m}f(\mathbf{x}^k)$ değerini üreten $\mathbf{x_k} \in \mathbb{R}^n$ olacaktır.

Böyle bir optimizasyon yönteminin çözümünde gündelik hayatta karşımıza bazı zorluklar çıkmaktadır. Bu zorluklardan bazıları aşağıda maddeler halinde verilmiştir.

• $f$ fonksiyonunun tanımının bilinmemesi: Günümüzde veri analizi ve makine öğrenmesi problemlerinin neredeyse tamamında öğrenme veri seti ve etiketler üzerinden yapılmaktadır. Makine öğrenmesi problemlerinde, herhangi bir verinin ($\mathbf{x}$) hangi etikete ($y$) sahip olduğu bilinse de, veriyi etikete taşıyan $y=f(\mathbf{x})$ fonksiyonu hiç bir zaman bilinmemektedir. Zaten makine öğrenmesi dediğimiz sürecin amacı $f: \mathbb{R^n} \rightarrow \mathbb{R}$ fonksiyonunun bulunması işlemidir.

• Eğer $f$ fonksiyonu yüksek dereceden bir fonksiyon ise $\nabla f(\mathbf{x})$ fonksiyonu da yüksek dereceden bir fonksiyon olacağından $\nabla f(\mathbf{x}^k) = 0$ çözümünü sağlayan $\mathbf{x}^k$ değerlerini bulmak oldukça zor olacaktır.

• İkinci adımda bahsedilen $\nabla f(\mathbf{x}^k) = 0$ problemi çözülebilse dahi, eşitliği sağlayan $\mathbf{x}^k$ değerleri sonsuz sayıda olabileceğinden $\min_{k=1,\dots,m}f(\mathbf{x}^k)$ probleminin çözümü, orjinal problemin çözümü kadar zor olacaktır.

Yukarıda sayılan nedenlerden ötürü $f(\mathbf{x})$ fonksiyonunun en küçüklemesi/büyüklemesi probleminin bilgisayarlar ile çözümü analitik yöntemler yerine iteratif yöntemler kullanılarak yapılmaktadır. Bu yazımızda değineceğimiz iteratif yöntemler literatürde İniş Yöntemleri (Descent Methods) olarak bilinen grubun altında yer almaktadır.

İniş Yöntemleri; rastgele seçilen bir $\mathbf{x_0}$ değerinden başlayarak, her adımda, $\mathbf{x_{k+1}} = \mathbf{x_k} + \eta_k d_k$ işlemi ile $\nabla f(\mathbf{x_k})$ fonksiyonunun sıfıra yakınsamasını sağlar.

Burada $\eta_k$ adım boyunu, $d_k$ ise iniş doğrultusunu göstermektedir. Herhangi bir $d \neq 0 \in \mathbb{R}^n$ vektörünün iniş doğrultusu olabilmesi için

\[\nabla^\intercal f(\mathbf{x}) d \lt 0 \tag{1}\]

şartını sağlaması gerekmektedir.

önsav: $d \in \mathbb{R}^n$ vektörünün bir iniş doğrultusu olması durumunda seçilen küçük bir $\epsilon>0$ değeri için $f(\mathbf{x}+\epsilon d) \lt f(\mathbf{x})$ olmak zorundadır.

ispat: $f$ fonksyinunun, $d$ yönündeki türevi aşağıdaki denklem ile tanımlanır.

\[\nabla_d f(\mathbf{x}) = \lim_{\epsilon\to 0^{+}} \frac{f(\mathbf{x}+\epsilon d) - f(\mathbf{x})}{\epsilon}\]

Burada $f$ türevlenebilir ise; $\nabla_d f(\mathbf{x})=\nabla_d f(\mathbf{x}) = \nabla^\intercal f(\mathbf{x}) d$ eşitliği geçerlidir. $d$ vektörünün iniş doğrultusu olabilmesi için $\nabla^\intercal f(\mathbf{x}) d \lt 0$ olması şartı bulunduğundan, yukarıda verilen limit ifadesinin de negatif olması gerekmektedir. Limitin payda kısmı $\epsilon \gt 0$ olduğundan pay kısmının $f(\mathbf{x}+\epsilon d) - f(\mathbf{x}) \lt 0$ olması gerekmektedir. Bu da ancak $f(\mathbf{x}+\epsilon d) \lt f(\mathbf{x})$ olması durumunda mümkündür.

Yukarıda verilen ispat aracılığıyla, $\eta_k = \epsilon$ ve $d_k=d$ iniş doğrultusunda bir vektör seçilmesi durumunda $f(\mathbf{x_{k+1}} = \mathbf{x_k} + \eta_k d_k) \lt f(\mathbf{x_k})$ olduğu, yani İniş Yönteminin her iterasyonda o anki $f(\mathbf{x_k})$ değerinden daha küçük bir $f(\mathbf{x_{k+1}})$ değeri bulduğu görülür. Bu iterasyonlar bulunan $f(\mathbf{x_k})$ değeri artık küçülmeyene kadar devam ettirilerek bir $f$ fonksiyonunun en küçük noktası bulunabilir.

Algoritmik olarak bu akış aşağıdaki şekilde özetlenebilir.

• İlklendirme: $\mathbf{x_0} \in \mathbb{R}^n$
• İterasyon: $k=0,1,\dots$ için
  • (a) Bir iniş yönü $d_k$ seç, öyle ki $\nabla^\intercal f(x) d_k \lt 0$ olsun
  • (b) Bir adım boyu $\eta_k$ belirle, öyle ki $f(\mathbf{x_k} + \eta_k d_k) < f(\mathbf{x_k})$ olsun
  • (c) $\mathbf{x_{k+1}} = \mathbf{x_k} + \eta_k d_k$ şeklinde güncelle
  • (d) Durma koşulu sağnadıysa dur, yoksa (a) adımına dön

Verilen akış incelendiğinde iniş yöntemine dayalı iteratif en küçükleme algoritmasında kritik iki adımın (a,b) olduğu görülmektedir. Bunlardan ilki $d_k$ iniş yönünün belirlenmesi, ikincisi ise yukarıdaki ispatta sabit kabul ettiğimiz $\eta_k$ adım aralığının belirlenmesi işlemidir. Bu iki parametrenin farklı yöntemlerle belirlenmesine dayanarak, literatürde çeşitli iniş yöntemi algoritmaları önerilmiştir. Bu yazımızda literatürde yaygın olarak kullanılan Gradyan İniş Yöntemi ve Kesin Doğru Arama iniş yöntemleri incelenecektir. İniş yöntemlerininin davranışlarını ve aradaki farkları daha iyi görebilmek adına yöntemlerin tanımı verildikten sonra basit bir optimizasyon problemi üzerinden yöntemin çalışması incelenecektir.

Örnek Problemin Analitik Çözümü

Elimizde $f(x,y) = x^2+2y^2$ ile verilen bir $f(\mathbf{x})$ fonksiyonu olduğunu varsayalım. Bu fonksiyon üzerinden $\min_{x,y} f(x,y)$ şartını sağlayan $x,y$ değerleri soruluyor olsun. Bildiğimiz üzere bir fonksiyonun yerel en küçük noktası birinci türevin sıfır, ikinci türevin pozitif olduğu noktadır.

Burada öncelikle $f(x,y)$ fonksiyonunun birinci türevine bakalım.

\[\nabla f(x,y) = \begin{bmatrix} \frac{\partial f(x,y)}{\partial x} \\ \frac{\partial f(x,y)}{\partial y} \end{bmatrix}= \begin{bmatrix} 2x \\ 4y \end{bmatrix}\]

Burada birinci türev sıfıra eşitlenirse; $\nabla f(x,y) = 0$ şartını sağlayan tek noktanın $x=0, y=0$ noktası olduğu görülür. Bu noktanın yerel en küçük nokta olup olmadığını görmek için $f(x,y)$ fonksiyonunun ikinci türevini alırsak:

\[\nabla^2 f(x,y) = \begin{bmatrix} \frac{\partial^2 f(x,y)}{\partial x \partial x} && \frac{\partial^2 f(x,y)}{\partial x \partial y}\\ \frac{\partial^2 f(x,y)}{\partial y \partial x} && \frac{\partial^2 f(x,y)}{\partial y \partial y} \end{bmatrix}= \begin{bmatrix} 2 & 0 \\ 0 & 4 \end{bmatrix}\]

elde edilir. $(0,0)$ noktası ikinci türevde yerine koyulursa elde edilen matrisin pozitif tanımlı (tüm özdeğerleri pozitif) olduğu görülür. Bu durumda $f(0,0)=0$ verilen $f$ fonksiyonunun en küçük noktasıdır denilir. Şimdi bu analitik çözümü iteratif iniş yöntemleri ile çözmeye çalışalım.

Gradyan İniş Yöntemi (Gradient Descent)

Gradyan iniş yöntemi iniş doğrultusu $d_k$ vektörünü, gradyanın tam tersi yönünde, $d_k=-\nabla f$ şeklinde seçmeyi önermektedir. Bu şekilde seçilen bir $d_k$ için

\[\nabla^\intercal f d = - \nabla^\intercal f \nabla f = -\lVert \nabla f) \lVert^2 \lt 0\]

olduğundan Denklem $\eqref{1}$ ile verilen iniş doğrultusu olma şartı sağlanmış olur. Gradyan İniş yöntemi iniş adım boyutu $\eta$ nın seçimi için bir yöntem önermemektedir.

Verilen örnek problemin Gradyan İniş Yöntemi ile çözümü için $\eta_k=0.25$ gibi sabit bir sayı olduğunu varsayalım. Bu durumda problem şu şekilde çözülecektir.

• İlklendirme:
  • $\mathbf{x_0} = \begin{bmatrix}2.0 \ 2.0 \end{bmatrix}$
• İterasyon 1
  • $d_0 = -\nabla f(x,y) = -\begin{bmatrix} 2 \times 2.0 \ 4 \times 2.0\end{bmatrix} = -\begin{bmatrix} 4.0 \ 8.0\end{bmatrix}$
  • $\eta_0 = 0.25$
  • $\mathbf{x_1} = \mathbf{x_0} + \eta_0 d_0 = \begin{bmatrix}2.0 \ 2.0 \end{bmatrix} - 0.25 \begin{bmatrix} 4.0 \ 8.0\end{bmatrix} = \begin{bmatrix} 1.0 \ 0.0\end{bmatrix}$
  • $f(\mathbf{x_1}) = x^2+2y^2 = 1^2 + 2 \times 0.0^2 = 1$
  • $\lVert \nabla f(\mathbf{x_1}) \lVert = 2$
• İterasyon 2
  • $d_1 = -\nabla f(x,y) = -\begin{bmatrix} 2 \times 1.0 \ 4 \times 0.0\end{bmatrix} = -\begin{bmatrix} 2.0 \ 0.0\end{bmatrix}$
  • $\eta_1 = 0.25$
  • $\mathbf{x_2} = \mathbf{x_1} + \eta_1 d_1 = \begin{bmatrix}1.0 \ 0.0 \end{bmatrix} - 0.25 \begin{bmatrix} 2.0 \ 0.0\end{bmatrix} = \begin{bmatrix} 0.5 \ 0.0\end{bmatrix}$
  • $f(\mathbf{x_2}) = x^2+2y^2 = 0.5^2 + 2 \times 0.0^2 = 0.25$
  • $\lVert \nabla f(\mathbf{x_2}) \lVert = 1.0$
• İterasyon 3
  • $d_2 = -\nabla f(x,y) = -\begin{bmatrix} 2 \times 0.5 \ 4 \times 0.0\end{bmatrix} = -\begin{bmatrix} 1.0 \ 0.0\end{bmatrix}$
  • $\eta_2 = 0.25$
  • $\mathbf{x_3} = \mathbf{x_2} + \eta_2 d_2 = \begin{bmatrix}0.5 \ 0.0 \end{bmatrix} - 0.25 \begin{bmatrix} 1.0 \ 0.0\end{bmatrix} = \begin{bmatrix} 0.25 \ 0.0\end{bmatrix}$
  • $f(\mathbf{x_3}) = x^2+2y^2 = 0.25^2 + 2 \times 0.0^2 = 0.0625$
  • $\lVert \nabla f(\mathbf{x_3}) \lVert = 0.5$

İterasyonlardan da görüldüğü üzere her iterasyon adımında $f(\mathbf{x_k})$ fonksiyonu geometrik olarak sıfıra yaklaşmaktadır. İterasyon adımlarına $\lVert \nabla f(\mathbf{x_k}) \lVert \lt 10^{-5}$ olana kadar devam edilirse (toplam 20 iterasyon) aşağıda verilen grafik oluşur.

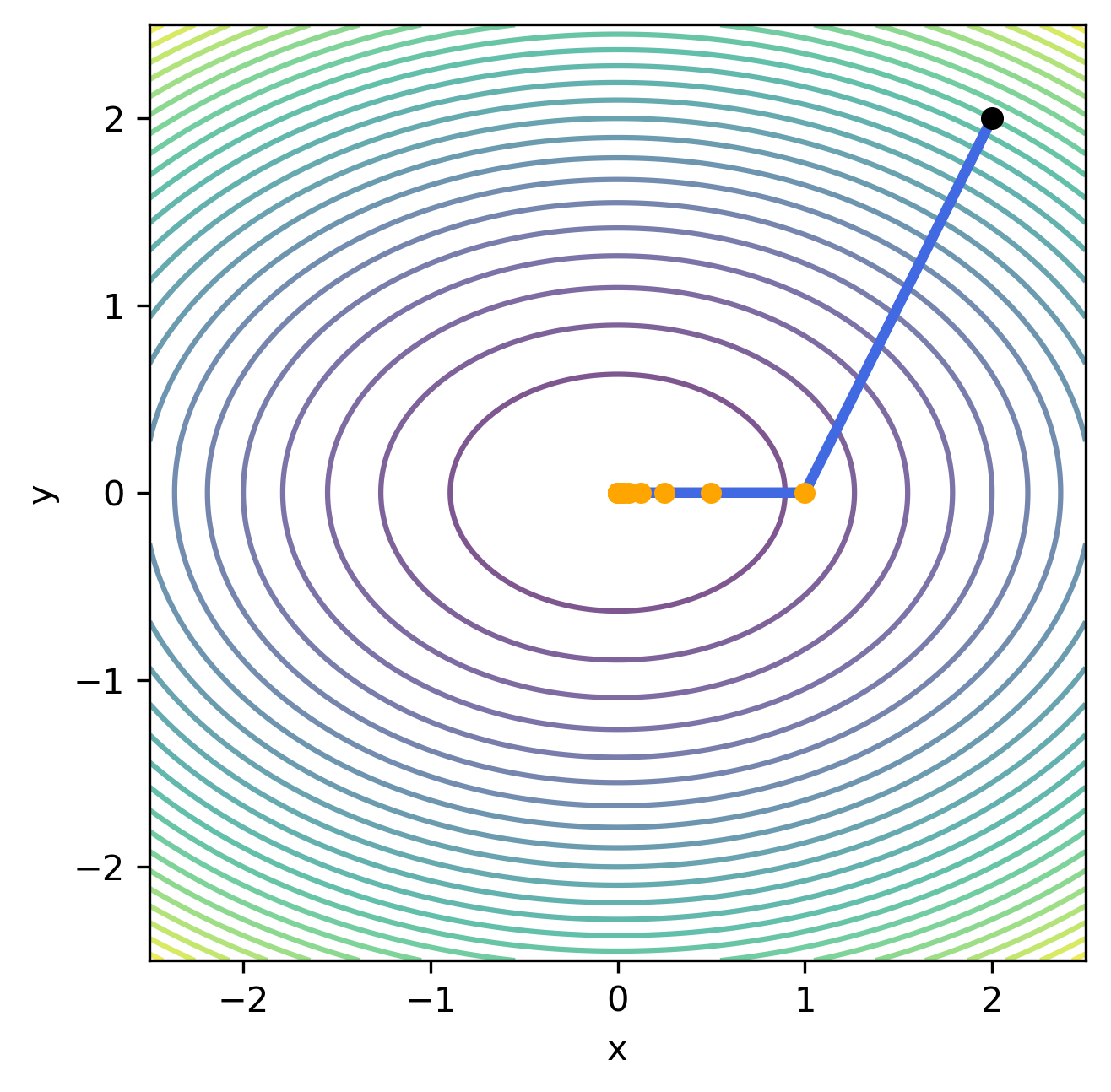
Verilen grafikte siyah ile gösterilen nokta iterasyonun başlangıç noktasını ($\mathbf{x_0}$) göstermektedir. Sarı ile gösterilen noktalar ise her adımda gidilen $\mathbf{x_k}$ noktalarını göstermektedir. Mavi ile gösterilen çizgi ise $d_k$ doğrultusunu göstermektedir.

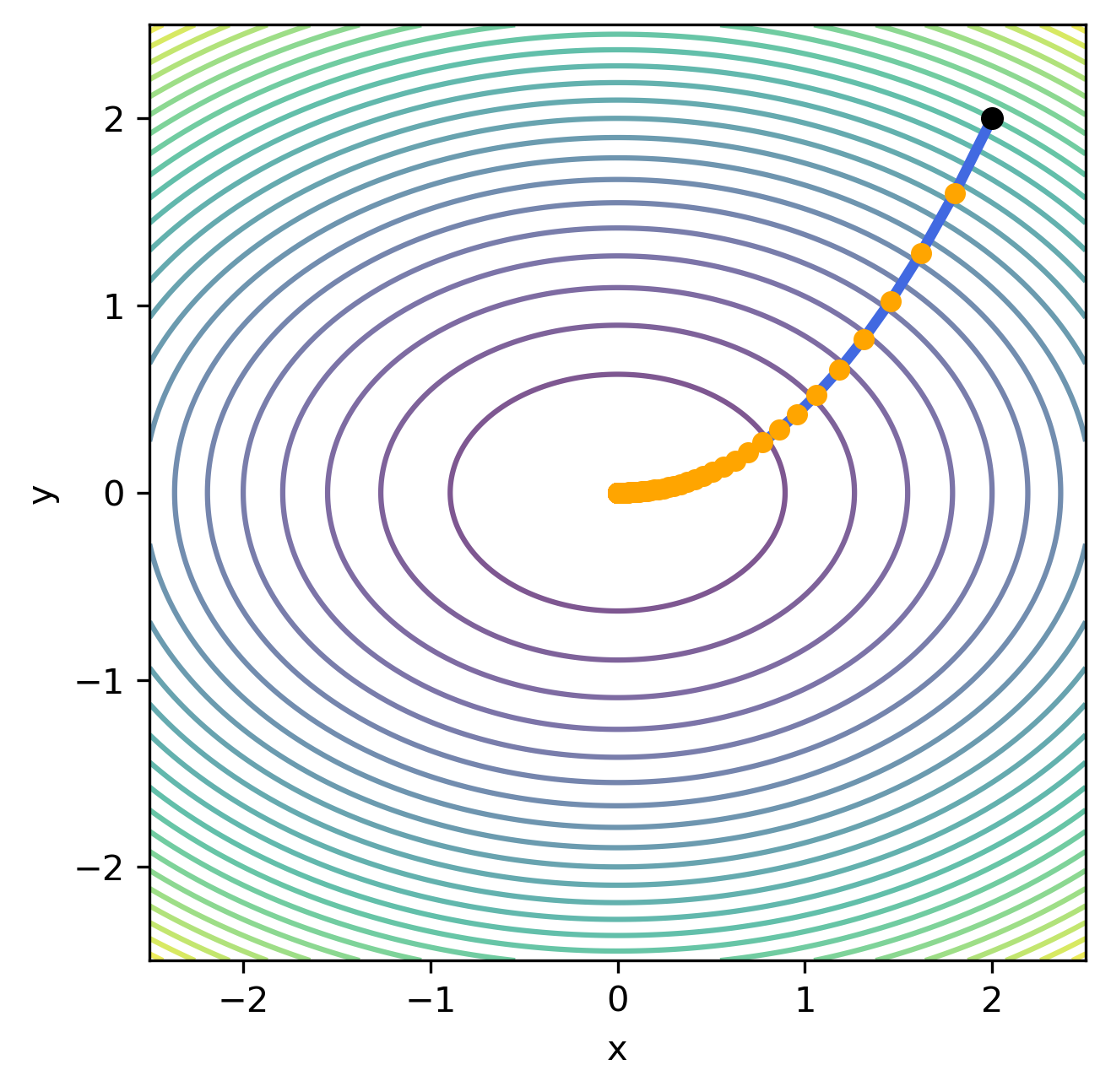
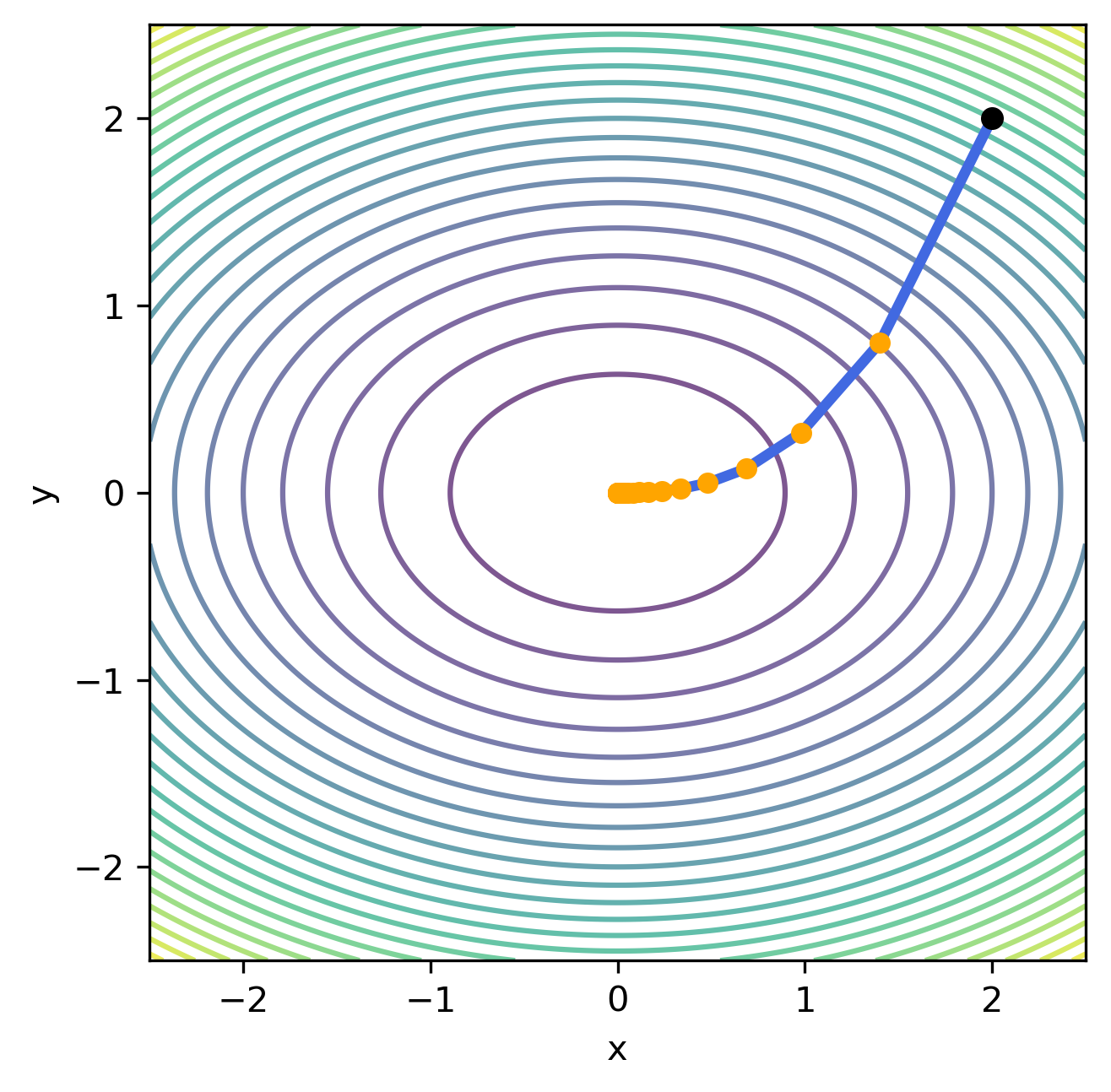
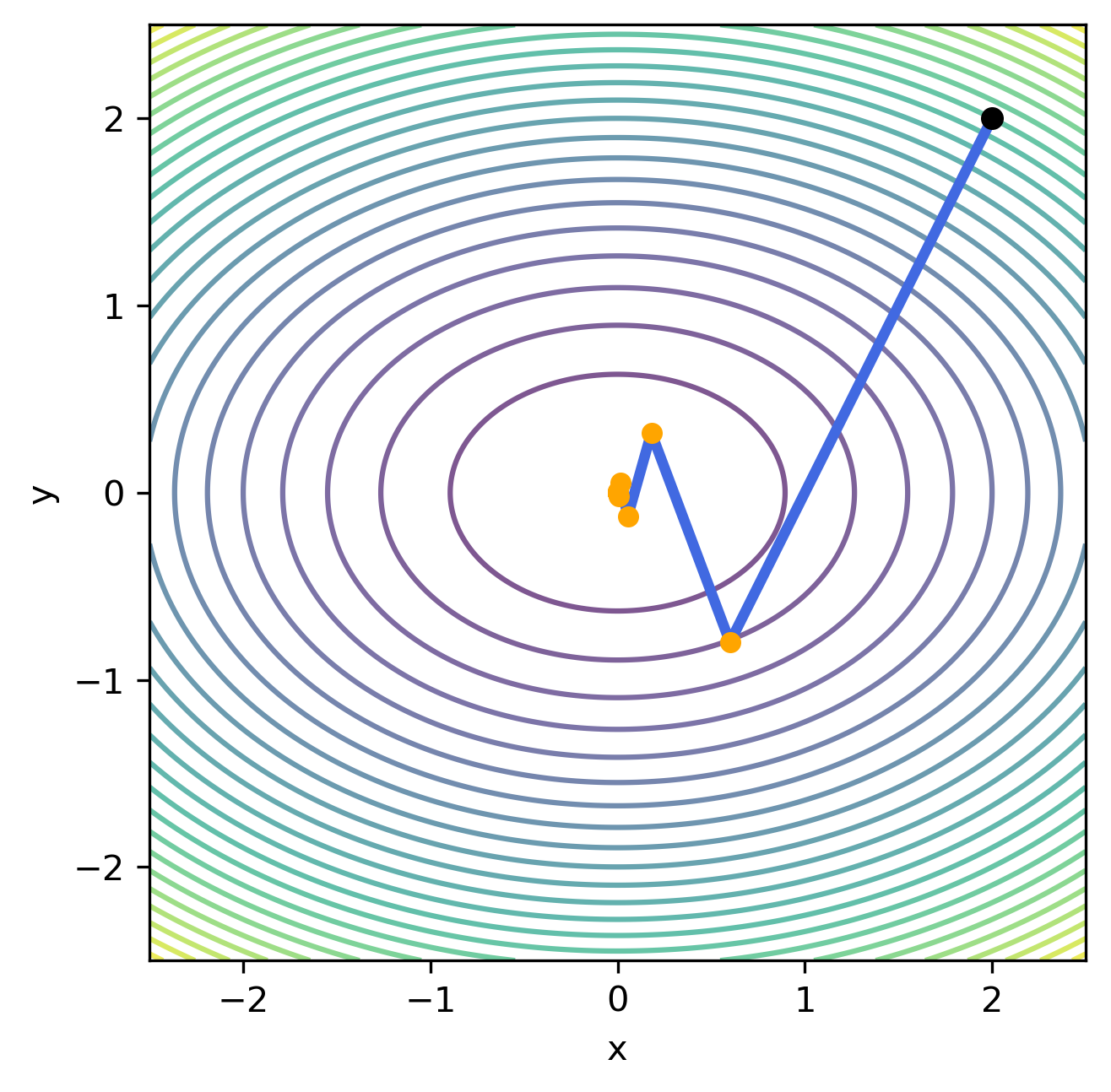
Gradyan iniş yönteminin çalışmasını etkileyen en önemli parametre $\eta$ adım boyutudur. Bu parametrenin etkisini incelemek için örnek problem farklı $\eta$ değerleri üzerinden çözülerek aşağıda verilen grafikler hazırlanmıştır.

$\eta=0.05$	$\eta=0.15$	$\eta=0.25$	$\eta=0.35$	$\eta=0.45$

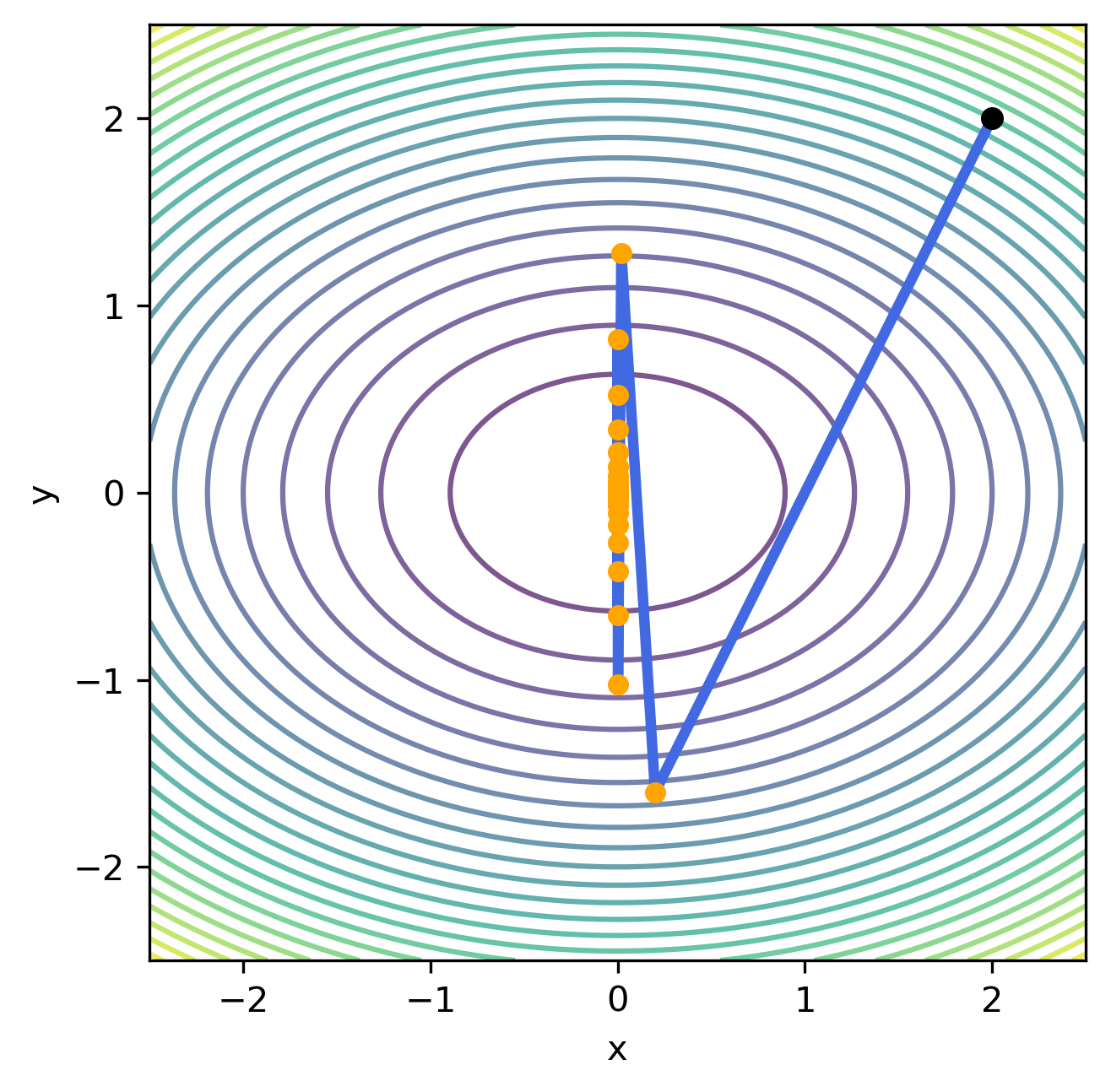Grafiklerden de görüldüğü üzere, küçük $\eta$ değerleri için yöntemin yakısaması uzun sayıda iterasyon gerektirirken, büyük $\eta$ değerleri için yöntemin hiç yakınsamama riski bulunmaktadır. Bu problemlerin önüne geçmek için gradyan iniş yöntemi ile birlikte sabit $\eta$ kullanmak yerine iterasyonlar arasında değişen bir adım boyutu kullanmak tercih edilmektedir. Bu adım boyutu genllikle, $\eta_k = \frac{\eta}{k}$ gibi, iterasyonun başlangıcında büyük adım boyları kullanmaya izin verirken, ilerleyen iterasyonlarda kullanılan adım boyunu kısaltacak şekilde seçilmektedir.

Kesin Doğru Araması (Exact Line Search)

Gradyan İniş yönteminde karşımıza çıkan $\eta$ adım boyutunun belirlenemesi problemine karşı önerilen bir yöntemdir. Yöntem her iterasyon adımında seçilen bir $d_k$ doğrultusu için en uygun $\eta_k$ adım boyunu bulmaya yönelik ikinci bir optimizasyon problemi tanımlar. Bu problem;

\[\eta_k = \arg \min_{\eta \geq 0} f(\mathbf{x_k} + \eta d_k) \tag{2}\]

şeklinde tanımlanır. Bu optimizasyon problemi sonucunda yöntem $\mathbf{x_k}$ noktasından, $d_k$ doğrultusunda ne uzunlukta bir adım $\eta_k$ atması durumunda $f$ fonksiyonunun en küçük değerine ulaştığını çözmeyi amaçlar.

Örnek problemimiz üzerinde Kesin Doğru Araması ile seçmemiz gereken adım boylarını hesaplamaya çalışalım. Örnek problemimizi ikinci dereceden türev (Hessian) matrisini kullanılarak aşağıda verilen şekilde yeniden yazabiliriz.

\[f(x,y) = x^2+2y^2=\frac{1}{2} \begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix}2 & 0 \\0 & 4\end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}\]

Burada işlem kolaylığı sağlaması açısından $\mathbf{x} = \left [x, y \right ]^\intercal$ ve $H=\nabla^2 f(\mathbf{x})$ değişkenleri kullanılarak problem düzenlenirse

\[f(\mathbf{x}) = \frac{1}{2} \mathbf{x}^\intercal H \mathbf{x}\]

fonksiyonu elde edilir. Bu fonksiyon Denklem $\eqref{2}$ ile verilen Kesin Doğru Araması optimizasyon probleminde yerine yazılırsa

\[\eta_k = \arg \min_{\eta \geq 0} \frac{1}{2} \left ( \mathbf{x_k + \eta d_k} \right ) ^\intercal H \left ( \mathbf{x_k + \eta d_k} \right )\]

problemi elde edilir. Burada en küçüklenmeye çalışılan ifadenin $g(\eta) = \frac{1}{2} \left ( \mathbf{x_k + \eta d_k} \right ) ^\intercal H \left ( \mathbf{x_k + \eta d_k} \right )$ türevi alınıp sıfıra eşitlenerek $\eta$ bulunabilir.

\[\begin{aligned} \nabla_{\eta} g(\eta) &= 0 \\ &= \nabla_{\eta} \left ( \frac{1}{2} \left ( \mathbf{x_k + \eta d_k} \right ) ^\intercal H \left ( \mathbf{x_k + \eta d_k} \right ) \right ) \\ &= \nabla_{\eta} \left ( \frac{\eta^2}{2}d_k^\intercal H d_k + \frac{1}{2}\mathbf{x_k}^\intercal H \mathbf{x_k} + \eta d_k^\intercal H \mathbf{x} \right ) \\ &= \eta d_k^\intercal H d_k + d_k^\intercal H \mathbf{x_k} \\ \eta &= -\frac{d_k^\intercal H \mathbf{x_k}}{d_k^\intercal H d_k} \end{aligned}\]

Denklem $\eqref{2}$ ten hatırlayacağımız üzere aranan $\eta$ değerinin pozitif olma şartı vardır. Yukarıda bulunan $\eta$ ifadesinde $H \mathbf{x_k} = \nabla f(\mathbf{x})$ olduğundan, eğer $d_k$ iniş doğrultusu ise ifadenin pay kısmı $-d_k^\intercal \nabla f(\mathbf{x}$) sıfırdan büyük olur. Payda kısmında bulunan $H$ Hessian matrisininde pozitif tanımlı olması durumunda $\eta \gt 0$ şartı sağlanmış olur.

Verilen örnek problemin Kesin Doğru Araması Yöntemi ile çözümü aşağıdaki şekilde olacaktır.

• İlklendirme:
  • \(\mathbf{x_0} = \begin{bmatrix}2.0 \\ 2.0 \end{bmatrix}\)
• İterasyon 1
  • \(d_0 = -\nabla f(x,y) = -\begin{bmatrix} 2 \times 2.0 \\ 4 \times 2.0\end{bmatrix} = -\begin{bmatrix} 4.0 \\ 8.0\end{bmatrix}\)
  • \(\eta_0 = -\frac{d_0^\intercal H \mathbf{x_0}}{d_0^\intercal H d_0} = -\frac{-80.0}{288.0}=0.277\)
  • \(\mathbf{x_1} = \mathbf{x_0} + \eta_0 d_0 = \begin{bmatrix}2.0 \\ 2.0 \end{bmatrix} - 0.277 \begin{bmatrix} 4.0 \\ 8.0\end{bmatrix} = \begin{bmatrix} 0.888 \\ -0.222\end{bmatrix}\)
  • \(f(\mathbf{x_1}) = x^2+2y^2 = 0.888^2 + 2 \times (-0.222)^2 = 0.888\)
  • \(\lVert \nabla f(\mathbf{x_1}) \lVert = 1.987\)
• İterasyon 2
  • \(d_1 = -\nabla f(x,y) = -\begin{bmatrix} 2 \times 0.888 \\ 4 \times -0.222\end{bmatrix} = -\begin{bmatrix} 1.776 \\ -0.888\end{bmatrix}\)
  • \(\eta_1 = -\frac{d_1^\intercal H \mathbf{x_1}}{d_1^\intercal H d_1} = -\frac{-3.95}{9.48}=0.416\)
  • \(\mathbf{x_2} = \mathbf{x_1} + \eta_1 d_1 = \begin{bmatrix} 0.888 \\ -0.222 \end{bmatrix} - 0.416 \begin{bmatrix} 1.776 \\ -0.888 \end{bmatrix} = \begin{bmatrix} 0.148 \\ 0.148\end{bmatrix}\)
  • \(f(\mathbf{x_2}) = x^2+2y^2 = 0.148^2 + 2 \times (0.148)^2 = 0.065\)
  • \(\lVert \nabla f(\mathbf{x_2}) \lVert = 0.662\)
• İterasyon 3
  • \(d_2 = -\nabla f(x,y) = -\begin{bmatrix} 2 \times 0.148 \\ 4 \times 0.148\end{bmatrix} = -\begin{bmatrix} 0.296 \\ 0.592\end{bmatrix}\)
  • \(\eta_2 = -\frac{d_2^\intercal H \mathbf{x_2}}{d_2^\intercal H d_2} = -\frac{-0.438}{1.580}=0.277\)
  • \(\mathbf{x_3} = \mathbf{x_2} + \eta_2 d_2 = \begin{bmatrix}0.148 \\ 0.148 \end{bmatrix} - 0.277 \begin{bmatrix} 0.296 \\ 0.592\end{bmatrix} = \begin{bmatrix} 0.065 \\ -0.016\end{bmatrix}\)
  • \(f(\mathbf{x_3}) = x^2+2y^2 = 0.065^2 + 2 \times (-0.016)^2 = 0.0048\)
  • \(\lVert \nabla f(\mathbf{x_3}) \lVert = 0.147\)

İterasyonlardan da görüldüğü üzere her iterasyon adımında $f(\mathbf{x_k})$ fonksiyonu Gradyan İniş Yönteminde göre çok daha hızlı bir şekilde sıfıra yaklaşmaktadır. İterasyon adımlarına $\lVert \nabla f(\mathbf{x_k}) \lVert \lt 10^{-5}$ olana kadar devam edilirse (toplam 12 iterasyon) aşağıda verilen grafik oluşur.

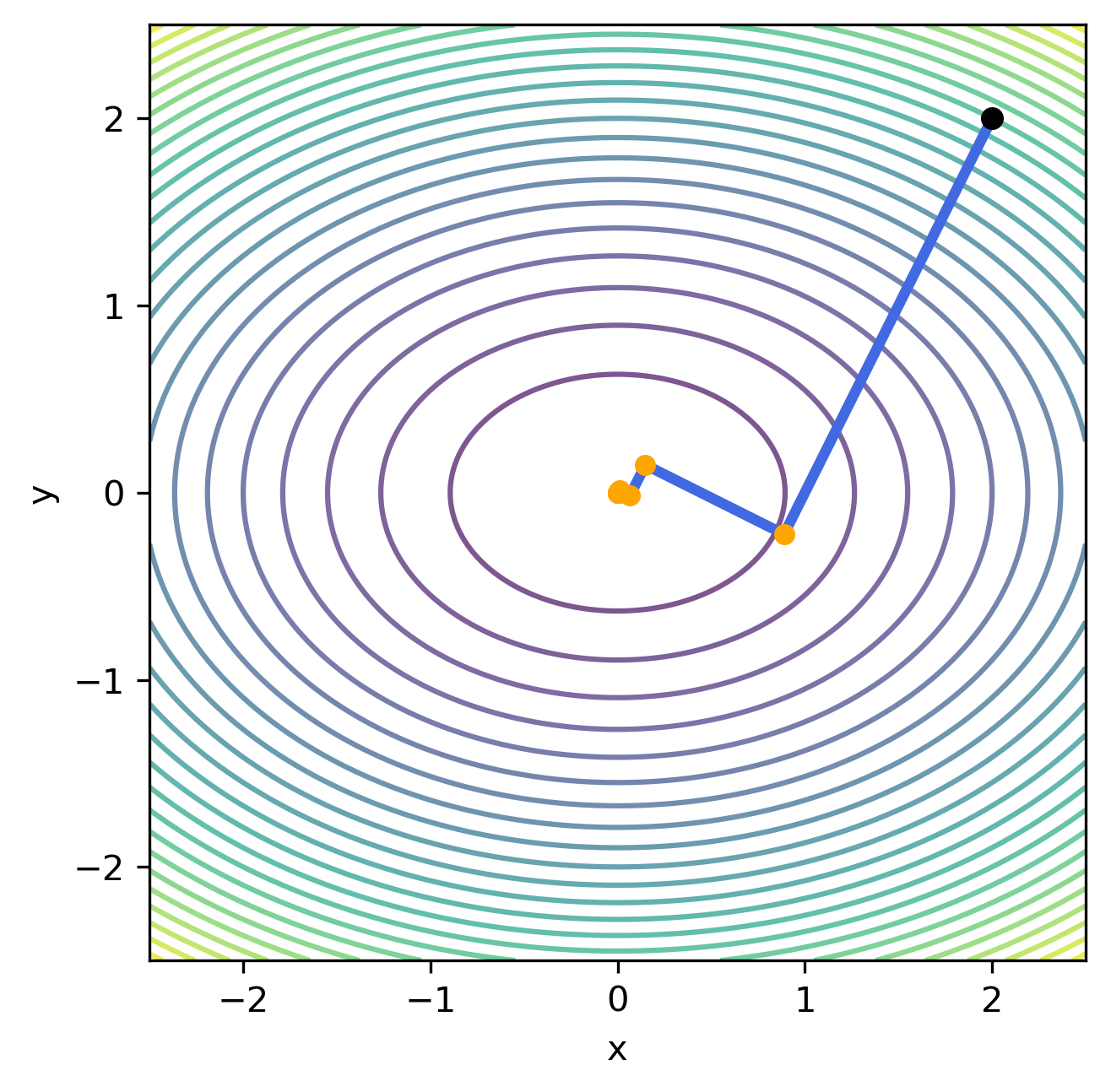
Verilen grafikte siyah ile gösterilen nokta iterasyonun başlangıç noktasını ($\mathbf{x_0}$) göstermektedir. Sarı ile gösterilen noktalar ise her adımda gidilen $\mathbf{x_k}$ noktalarını göstermektedir. Mavi ile gösterilen çizgi ise $d_k$ doğrultusunu göstermektedir. Kesin doğru araması $\eta$ adım boyunun bulunması için optimum çözümü önerse de $H=\nabla^2 f(\mathbf{x})$ ikinci türev bilgisini gerektirdiğinden kısıtlı bir kullanım alanına sahiptir.

Yazıda yer alan analizlerin yapıldığı kod parçaları, görseller ve kullanılan veri setlerine imlab_optimization_using_gradient_methods GitHub sayfası üzerinden erişilebilir.

Referanslar

• Beck, Amir. Introduction to nonlinear optimization: Theory, algorithms, and applications with MATLAB. Vol. 19. Siam, 2014.

• Alpaydin, Ethem. Introduction to machine learning. MIT press, 2014.