Kaynak konumlandırma (Source Localization), konumu bilinmeyen bir kaynağın, konumu bilinen refarans noktalarından alınan ölçümler sonucunda konumuna dair bir kestirimde bulunulması işlemidir. Biyomedikal görüntülemede beyne yerleştirilen elektrotlardan alınan sinyallerin şiddeti kullanılarak beyinde sinyali yayan bölgenin tespit edilmesi, akustik uygulamalarında mikrofon dizileri tarafından alınan sesin şiddetine bağlı olarak ses kaynağının tespiti gibi pek çok farklı uygulama alanına sahiptir. Bu yazımızda basit bir kaynak konumlandırma probleminin önceki yazılarımızda incelediğimiz Gradyan İniş Yöntemleri ile nasıl çözülebileceğini inceleyeceğiz.
Kaynak konumlandırma başlık itibariyle hepimize uzak bir konu gibi görünse de aslında günlük hayatımızda da sıklıkla duyduğumuz bir kullanım alanına sahiptir. Örneğin kullandığımız cep telefonlarının konumu, herhangi bir ilave yazılım veya donanıma ihtiyaç duyulmadan bu yöntem ile tespit edilebilmektedir. Bu yazımızda inceleyeceğimiz örnek de anlaşılır olması açısından bu uygulama örneği üzerinden anlatılacaktır.
Örnek olarak, bir mobil telefon şirketinin bölgeye yerleştirdiği üç baz istasyonu ($A$,$B$ ve $C$) olduğunu varsayalım. Konumu bulunmak istenen kullanıcının ($X$) telefonu ile bölgeye girmesi durumunda, telefon ile üç baz istasyonu arasında bir iletişim kurulacak ve bu iletişim sonucunda baz istasyonları telefondan gelen sinyalin gücünü ölçebilecektir. Sinyalin gücü ile uzaklığı arasındaki ilişki kullanılarak kullanıcının üç baz istasyonuna olan uzaklıklarının ($d_a$, $d_b$ ve $d_c$) olarak belirli bir hata ile tahmin edildiğini varsayalım. Bu durum grafiksel olarak aşağıdaki şekilde görselleştirilmiştir.
Verilen problemde amacımız bilinen baz istasyonu konumları ($P_a$,$P_b$ ve $P_c$) ve kestirilen uzaklıkları ($d_a$, $d_b$ ve $d_c$) kullanarak kullanıcının konumunu ($P_x$) bulmaktır. Bu problem özelinde; baz istasyonu konumlarının $P_a=(3,9)$, $P_b=(1,1)$, $P_c=(9,2)$ olduğunu ve kestirilen uzaklıkların $d_a=6$, $d_b=4$, $d_c=5$ şeklinde hesaplandığını varsayalım.
Verilen problem ilk bakışta üçgen eşitlikleri veya analitik yöntemler ile çözülebilir gibi görünse de, problemde bilinen $d$ mesafelerinin belirli bir hata ile kestirildiği unutulmamalıdır. Bu nedenle $P_x$ konumunda $d$ mesafesinin kestiriminden kaynaklanan bir hata olması muhtemeldir. Problemi optimizasyon problemi olarak yazarken amacımzı bu hatayı en küçükleyen $\hat{P_x}$ kestirimini bulmak olacaktır.
Problem tanımı gereği, $\lVert P_a-P_x \lVert \approx d_a$, $\lVert P_b-P_x \lVert \approx d_b$ ve $\lVert P_c-P_x \lVert \approx d_c$ yazılabilir. Bu durumda herhangi bir $P$ konumu için oluşacak ortalama karesel hata şu şekilde ifade edilebilir.
\[f(P) = \frac{1}{2} \sum_{i \in S} (\lVert P-P_i \lVert - d_i)^2 \tag{1}\]Verilen denklemde $S=\{ a,b,c \}$ problemde verilen bilinen noktaları göstermektedir. Denklem $\eqref{1}$ ile verilen hata fonksiyonu incelendiğinde, fonksiyonun en küçük değerini $P=P_x$ olduğunda aldığı görülür. $P=P_x$ seçilmesi durumunda oluşan hata $d$ konum kestirim hatalarının karesel toplamının yarısı kadar olacaktır.
Problemin çözümü için $f(P)$ fonksiyonu en küçükleyen $\hat{P_x} = \arg \min_{P} f(P)$ noktasının bulunması gerekmektedir. Bu değer Gradyan İniş Yöntemleri ve Lagrange Çarpanları yazılarımızda değindiğimiz üzere $C$ fonksiyonun gradyanını sıfıra eşitleyerek bulunur. Gradyan hesaplamasında kolaylık sağlaması açısından işlemlere başlamadan $g_i(P) = \lVert P-P_i \lVert$ tanımlamasını yapalım. Bu tanım kullanılarak $\nabla f$ aşağıdaki şekilde yazılabilir.
\[\begin{aligned} \nabla f(P)&=\nabla \left ( \frac{1}{2} \sum_{i \in S} \left ( g_i(P) -d_i \right )^2 \right )\\ &= \sum_{i \in S} \nabla g_i(P) \left ( g_i(P) -d_i \right )\\ &= \sum_{i \in S} \nabla g_i(P) g_i(P) - \sum_{i \in S} \nabla g_i(P) d_i \end{aligned} \tag{2}\]Elde edilen eşitlikten de görüldüğü üzere, hesaplamaya devam edebilmek için $g_i(P)$ fonksiyonunun gradyanına ihtiyaç duyulmaktadır. Bu hesaplama aşağıdaki şekilde yapılabilir.
\[\begin{aligned} \nabla g_i(P)&= \nabla \lVert P - P_i \lVert\\ &= \nabla \left( \sum_{j=1}^n \left ( P_j - P_{ij} \right )^2 \right)^{\frac{1}{2}}\\ &= \frac{1}{2} \left( \sum_{j=1}^n \left ( P_j - P_{ij} \right )^2 \right)^{-\frac{1}{2}} \left( \sum_{j=1}^n 2(P_j - P_{ij}) \frac{\partial (P_j - P_{ij})}{\partial P}\right)\\ &= \frac{\sum_{j=1}^n (P_j - P_{ij}) \frac{\partial (P_j - P_{ij})}{\partial P}}{\left( \sum_{j=1}^n \left ( x_j - P_{ij} \right )^2 \right)^{\frac{1}{2}}}\\ &= \frac{P - P_i}{\lVert P - P_i \lVert} \end{aligned} \tag{3}\]Denklem $\eqref{3}$ ile elde edilen eşitlik Denklem $\eqref{2}$ da yerine konularsa;
\[\begin{aligned} \nabla f(P)&=\sum_{i \in S} \nabla g_i(P) g_i(P) - \sum_{i \in S} d_i \nabla g_i(P) \\ &= \sum_{i \in S} \frac{P - P_i}{\lVert P - P_i \lVert} {\lVert P - P_i \lVert} - \sum_{i \in S} d_i\frac{P - P_i}{\lVert P - P_i \lVert} \\ &= \sum_{i \in S} \left(P - P_i\right) - \sum_{i \in S} d_i\frac{P - P_i}{\lVert P - P_i \lVert} \\ &= m P - \sum_{i \in S} P_i - \sum_{i \in S} d_i\frac{P - P_i}{\lVert P - P_i \lVert} \end{aligned} \tag{4}\]bulunur. Burada $m$ verilen nokta sayısını ($m=3$) göstermektedir. Bulunan $\nabla f(P)$ ifadesi kullanılarak, $\eta_k=\frac{1}{m}$ seçilen En Dik İniş Yöntemi ile çözüm aşağıdaki şekilde hesaplanır.
\[\begin{aligned} P_{k+1} &= P_k - \eta_k \nabla f(P_k)\\ &= P_k - \frac{1}{m} \left( m P_k - \sum_{i \in S} P_i - \sum_{i \in S} d_i\frac{P_k - P_i}{\lVert P_k - P_i \lVert} \right)\\ &= \frac{1}{m} \left( \sum_{i \in S} P_i + \sum_{i \in S} d_i\frac{P_k - P_i}{\lVert P_k - P_i \lVert} \right) \end{aligned} \tag{5}\]Elde edilen iteratif çözümün gerçeklenmesi için C dilinde aşağıdaki kod parçası yazılmıştır.
// set the given parameters
float Pi[3][2] = { {3.0f,9.0f}, {1.0f,1.0f}, {9.0f,2.0f} };
float di[3] = {6.0f, 4.0f, 5.0f};
// set the starting position of the X to somewhere
float x[2] = {0.0f};
// continue until the error is no more decreasing
float difference = 0;
do
{
float xnew[2] = {0.0f};
// compute \sum_{i \in S} P_i + \sum_{i \in S} d_i\frac{P_k - P_i}{\lVert P_k - P_i \lVert}
int i = 0, j = 0;
for(j = 0; j < n; j++)
{
for(i = 0; i < m; i++)
{
xnew[j] += (Pi[i][j] + di[i] * (x[j] - Pi[i][j]) / diffnorm(x, Pi[i], n)) / m;
}
}
// now compute the difference between the xnew and x, and assign x = xn
difference = diffnorm(x, xnew, n);
memcpy(x, xnew, n * sizeof(float));
} while(difference > 1e-3);
Yazılan kod parçası $P_0=(0,0)$ ve $P_0=(10,10)$ gibi farklı iki başlangıç noktasından, elde edilen yeni konum $P_{k+1}$ ile eski konum $P_k$ arasındaki fark $10^{-3}$ ten küçük olana kadar çalıştırıldığında, toplam $17$ adımda aşağıdaki görselde verilen adımları izleyerek $P_x=(4.24, 3.20)$ noktasına ulaşmaktadır.
| Başlangıç Noktası $P_0=(0,0)$ | Başlangıç Noktası $P_0=(10,10)$ |
|---|---|
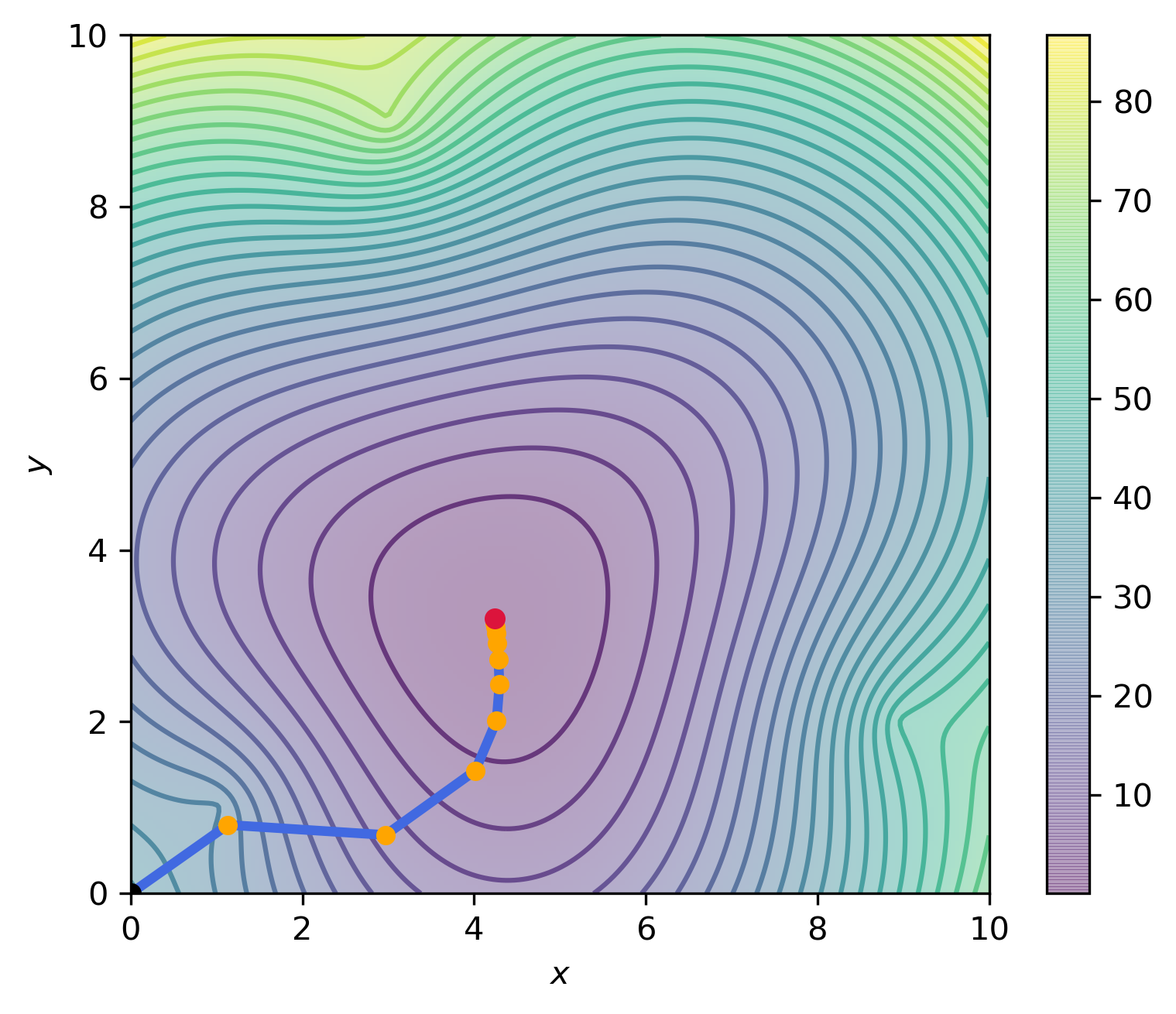 |
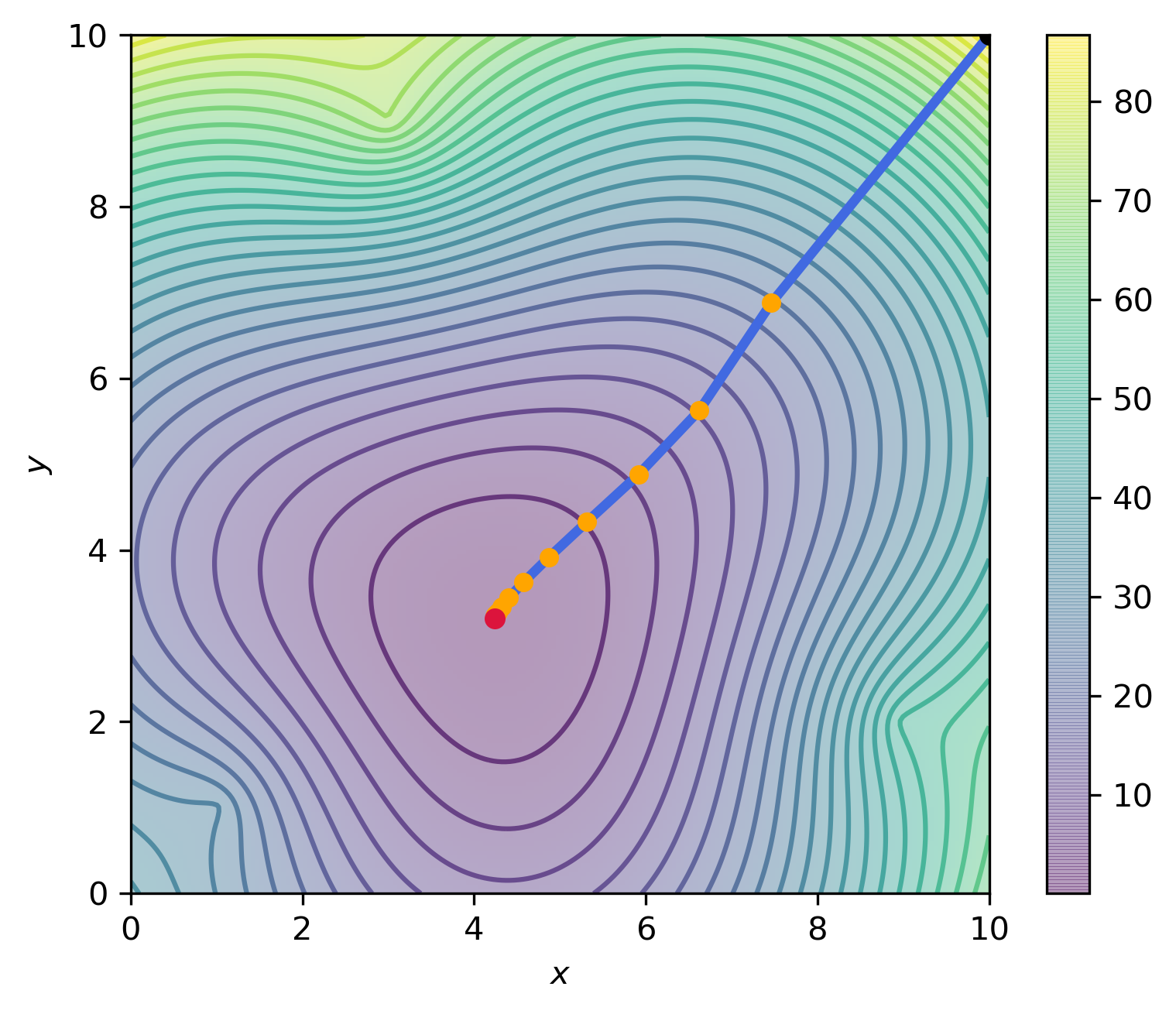 |
Verilen grafiklerde, arka plan renkleri ve kontur çizgileri $P=(x,y)$ seçilmesi durumunda elde edilecek hatayı göstermektedir. Siyah ile işaretlenen nokta iterasyonun başlangıç noktasını, kırmızı nokta ise iterasyonlar sonucunda ulaşılan noktayı göstermektedir. Turuncu ile gösterilen noktalar her iterasyon sonucunda gidilen yeni noktayı göstermektedir.
Yazıda yer alan analizlerin yapıldığı kod parçaları, görseller ve kullanılan veri setlerine source_localization GitHub sayfası üzerinden erişilebilirsiniz.
Referanslar
- Beck, Amir. Introduction to nonlinear optimization: Theory, algorithms, and applications with MATLAB. Vol. 19. Siam, 2014.
