Perspektif nesnenin bulunduğu konuma bağlı olarak, gözlemcinin gözünde bıraktığı etkiyi (görüntüyü) 2 boyutlu bir düzlemde canlandırmak için geliştirilmiş bir iz düşüm tekniğidir. Rönesans döneminde Masaccio’ nun resimlerinde kullanmaya başladığı teknik günümüzde gerçekçi çizimler oluşturmak için olmazsa olmazlardandır. Ancak olayı görüntü işleme açısından ele aldığımızda perspektif genellikle işlerimizi zorlaştıran bir etkiye sahiptir. Amaç nesne tanıma veya sınıflandırma olduğunda nesnenin hangi açıdan görüntülendiğinin bir önemi olmamalıdır.
Örneğin standart bir karakter tanıma uygulamasına görüntü olarak verilen “cescript, “cescript” veya ʇdıɹɔsǝɔ görüntüleri aynı kelime olmalarına rağmen bilgisayar tarafından her seferinde farklı olarak okunacaktır. İşte perspektif dönüşümü bu noktada devreye girerek verilen görüntü üzerindeki ölçekleme, yayma, dönme ve kayma gibi etkileri kaldırabilmemizi sağlar.
Perspektif düzeltmede amaç kişinin veya nesnenin konum değiştirmesi sonucu oluşacak etkiyi betimleyebilmektir. Bu işlem sayesinde görüntü oluştuktan sonra dahi belirli kısıtlar içerisinde resme baktığımız açıyı değiştirebiliriz. Algoritma karakter tanıma uygulamalrında (Cam Scanner gibi) çekilmiş bir görüntüyü belirli kalıplar içerisine oturmada, plaka tanıma, yüz tanıma gibi uygulamalarda normalizasyon sırasında sıklıkla kullanılmaktadır.
Aşağıda verilen matriste $x$,$y$ herhangi bir koordinat değeri olmak üzere, $x’$ ve $y’$ bu iki değerin dönüşüm sonrası değerlerini göstermektedir. Matris gösterimindeki a değerlerinin her birinin özel bir anlamı vardır.
\[\begin{bmatrix} x'z \\ y'z \\ z \end{bmatrix} \begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{bmatrix} \begin{bmatrix} x\\ y\\ 1\\ \end{bmatrix}\]Şimdi basitlik olması için bazı $a$ değerlerini $0$ kabul ederek elde edeceğimiz $x’$ ve $y’$ değerlerini yorumlamaya çalışalım. Anlaşılması en kolay durum ile incelememize başlayabiliriz: $a_{12}=a_{13}=a_{22}=a_{23}=a_{31}=a_{32} = 0$ ve $a_{11}=a_{22}=a_{33} = 1$. Bu durumda $x’ = x$ ve $y’=y$ olacaktır. Yani yeni oluşan görüntüdeki her bir nokta olduğu yerde kalacaktır. (Aynalama)
Öteleme
Diğer basit bir durum ise $a_{12}=a_{22}=a_{31}=a_{32} = 0$ ve $a_{11}=a_{22}=a_{33} = 1$ durumudur. Bu durumda yeni koordinat değerleri $y’ = y + a_{23}$, $x’ = x + a_{13}$ şeklinde olacaktır. Yani yeni görüntüdeki herbir nokta $a_{13}$ kadar sağa ve $a_{23}$ kadar aşağıya kayacaktır.
Ölçekleme
Ölçekleme işlemi için $a_{12}=a_{13}=a_{22}=a_{23}=a_{31}=a_{32} = 0$ ve ${a_{33}} = 1$ seçilerek şu durum elde edilir: $y’ = a_{22} y$ , $x’ = a_{11} x$. İfadenin daha anlaşılır olması için $a_{22}=1,a_{11}=2$ seçelim, bu durumda yeni oluşan resimde $y$ değerleri değişmezken, $x=10$ daki bir nokta $x’=20$ ye, $x=20$ deki bir nokta $x’=40$ a … şeklinde her bir $x$ noktası $2$ katına gitmekte yani resim $x$ ekseninde iki kat ölçeklenmektedir.
Döndürme
Döndürme işlemi $a_{11},a_{12},a_{21},a_{22}$ değerlerinin özel şekilde seçilmesi ile yapılır. Bu seçim döndürme açısı $\theta$ ya bağlı olarak şu şekilde ifade edilir: $a_{11} = \cos(\theta)$ , $a_{12} =-\sin(\theta)$ , $a_{21} = \sin(\theta)$ , $a_{22} = \cos(\theta)$. İnceleme yapabilmemiz için yine basit olarak $\theta$ değerini $180$, $a_{13},a_{23},a_{31},a_{32} = 0$ ve $a_{33} = 1$ seçelim. $\cos(180)=-1$ ve $\sin(180) = 0$ olduğu göz önünde bulundurularak dönüşüm sonrası değerlerimiz $x’ = -x$, $y’ = -y$ şeklinde olacaktır. Yani yeni görüntüde $y$ noktaları $-y$, $x$ noktası $-x$ noktasına taşınacak ve görüntü orijine göre simetrisi alınmış yani $180$ derece döndürülmüş olacaktır.
Daha karmaşık durumlar için ilk olarak $a_{13},a_{23}$ değerlerinin sıfırdan farklı olduğu durumlar incelenebilir. Bu durumda $x’$ değerinde $y$, $y’$ değerinde ise $x$ ekseninin etkisi görünecektir. Daha karmaşık bir durum ise perspektif düzeltmenin temeli olan $a_{31},a_{32}$ değerlerini sıfırdan farklı seçmektir. Bu durum görüntüdeki uzaklık etkisini $x’$ ve $y’$ değerlerine yayarak gözde üç boyut etkisini yaratan bükümü düzeltmeyi sağlar.
Bu yazımda basit örneklerle başlık halinde de verdiğim üç dönüşümü (Öteleme-Ölçekleme-Döndürme) örneklerle incelemeye çalışacağım. Dönüşüm için yazılan kodu inceleyerek başlayalım.
//a11 = T[0]; a12 = T[3]; a13 = T[6];
//a21 = T[1]; a22 = T[4]; a23 = T[7];
//a31 = T[2]; a32 = T[5]; a33 = T[8];
//x' = (x*a11 + y*a12 + a13) / z';
//y' = (x*a21 + y*a22 + a23) / z';
//z' = (x*a31 + y*a32 + a33);
uint8_t *in_data = data(uint8_t, in);
uint8_t *out_data = data(uint8_t, out);
// Affine
float *a = data(float, T);
int d, w, h;
for(h=0; h < height(out); h++)
{
for(w=0; w < width(out); w++)
{
double zp = w*a[6] + h*a[7] + a[8];
// if the z zero, continue
if(equal(zp, 0, 0.00001)) { continue; }
int x = (w*a[0] + h*a[1] + a[2]) / zp;
int y = (w*a[3] + h*a[4] + a[5]) / zp;
// check whether the x,y is outside the image
if( (x < 0) || (y < 0) || (x > width(out)-1) || (y > height(out)-1) ) { continue; }
for(d=0; d < channels(in); d++)
{
out_data[channels(out)*(x+y*width(out)) + d] = in_data[ channels(in)*(w+width(in)*h) + d];
}
}
}
Peki bu kadar mı?
Değil tabi ki :) Şu ana kadar okuduğunuz yazı içerisinde dikkatinizi bir noktanın özellikle çekmesini istemiştim. Ölçekleme kısmında verdiğim örnekte katsayının iki seçilmesi durumunda resimdeki her bir noktanın iki katına gittiğini söylemiştim. Aynı örnekte durumu yeni oluşan resim açısından ele alırsak, $x=1,x=3,\cdots$ gibi noktalar hiçbir $x,y$ çifti için bir değere sahip olamayacaktır. Bu yüzden oluşan resimde siyah noktalar (bu örnek için yatay çizgiler) oluşacaktır. Bunu engellemek için şöyle bir yöntem izleyebiliriz.
\[\begin{bmatrix} xz \\ yz \\ z \end{bmatrix} \begin{bmatrix} ia_{11} & ia_{12} & ia_{13}\\ ia_{21} & ia_{22} & ia_{23}\\ ia_{31} & ia_{32} & ia_{33}\\ \end{bmatrix} \begin{bmatrix} x'\\ y'\\ 1\\ \end{bmatrix}\]Yöntem ilk kısımda anlatılan yöntem ile aynı görünmesine karşılık, bu sefer çıktı görüntüsü üzerindeki bir noktanın $(x’,y’)$ girdi görüntüsü üzerinde nereden geldiğini aradığımızdan $(x,y)$ çıktı görüntüsü üzerinde hiç bir boş nokta kalmayacaktır. Kod üzerinde yapacağımız en önemli değişim a katsayıları yerine ia katsayılarını bulma kısmında olacaktır. Matrissel şekilde gösterilen $ia$ katsayıları $a$ katsayılarından oluşan matrisin tersine ait elemanlardır. Matris tersi bulma işlemini başka bir yazımda anlatmayı planladığımdan bu kısmı geçerek yeni yönteme ait kodları paylaşıyorum.
//ia11 = T[0]; a12 = T[3]; a13 = T[6];
//ia21 = T[1]; a22 = T[4]; a23 = T[7];
//ia31 = T[2]; a32 = T[5]; a33 = T[8];
//x' = (x*ia11 + y*ia12 + ia13) / z';
//y' = (x*ia21 + y*ia22 + ia23) / z';
//z' = (x*ia31 + y*ia32 + ia33);
uint8_t *in_data = data(uint8_t, in);
uint8_t *out_data = data(uint8_t, out);
// Affine
float *ia = data(float, iT);
int shidx, d, w, h;
for(h=0; h < height(out); h++)
{
shidx = h*width(out);
for(w=0; w < width(out); w++)
{
double zp = w*ia[6] + h*ia[7] + ia[8];
// if the z zero, continue
if(equal(zp, 0, 0.00001)) { continue; }
int x = (w*ia[0] + h*ia[1] + ia[2]) / zp;
int y = (w*ia[3] + h*ia[4] + ia[5]) / zp;
// check whether the x,y is outside the image
if( (x < 0) || (y < 0) || (x > width(in)-1) || (y > height(in)-1) ) { continue; }
for(d=0; d < channels(in); d++)
{
out_data[channels(out)*(w+shidx) + d] = in_data[ channels(in)*(x+width(in)*y) + d];
}
}
}
Dikkat edilecek olursa kodlamadaki tek değişimin T matrisi yerine iT olmadığı görülür. Bahsettiğim üzere bu değişim sonrasında for döngülerimizi çıkış görüntüsü üzerindeki koordinatlarda döndüreceğimizden x ve y (yani x’ ve y’) değerleri giriş görüntüsünde yerine yazılacaktır. Artık basitten karmaşığa doğru örneklerimize geçebiliriz.
| Orjinal İmge | 45° Döndürme | 90° Döndürme | 45° Döndürme ve Yarıya Ölçekleme |
|---|---|---|---|
 |
 |
 |
 |
rot2tform(128, 128, 0, 1.0) |
rot2tform(128, 128, 45, 1.0) |
rot2tform(128, 128, 90, 1.0) |
rot2tform(128, 128, 45, 0.5) |
| \(T= \begin{bmatrix} 1.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 1.0 \end{bmatrix}\) | \(T= \begin{bmatrix} 0.7 & -0.7 & 128.0 \\ 0.7 & 0.7 & -53.0 \\ 0.0 & 0.0 & 1.0 \end{bmatrix}\) | \(T= \begin{bmatrix} 0.0 & -1.0 & 256.0 \\ 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 \end{bmatrix}\) | \(T= \begin{bmatrix} 1.4 & -1.4 & 128.0 \\ 1.4 & 1.4 & -234.0 \\ 0.0 & 0.0 & 1.0 \end{bmatrix}\) |
Yukarıda farklı dönüşüm parametreleri için elde edilen sonuçlar verilmiştir. Sonuçlar üretilirken imlab kütüphanesinde yer alan ve bir merkez noktası etrafında dönme ve ölçekleme yapabilmek için gereken dönüşüm matrisini hesaplayan rot2tform fonksiyonu kullanılmıştır. Bu fonksiyonun ürettiği dönüşüm matrisleri de tabloda ilgili sütunların altında verilmiştir.
Son söz olarak perspektif düzeltmedeki katsayıların otomatik bulunmasından bahsedebiliriz. Bu yazıyı yazmamdaki esas neden sudoku çözücü için gerekli olan perspektif düzeltmesinin nasıl yapılacağını anlatmaktı. Bir önceki yazımı okuduysanız, sudoku karesinin karşıdan çekilmediği durumlarda ne olacağını merak etmiş olabilirsiniz. Böyle bir durumla karşılaşmamız durumunda gerekli dönüşüm katsayılarını otomatik olarak belirleyerek dönüşüm yapmamız gerekecektir.
Perspektif Dönüşüm Katsayılarının Elde Edilmesi
Parametrelerin otomatik olarak çıkarılması için bir kaç matris bölmesi işlemi gerekmektedir. Böylece girdi olarak verilen bir görüntü otomatik olarak kolaylıkla hizalanabilmektedir. Perspektif dönüşümünün bir matris çarpması ile yapıldığını biliyoruz. Dönüşüm için kullandığımız matrisi işlemlerimiz için tekrar yazalım.
\[\begin{bmatrix} x'z \\ y'z \\ z \end{bmatrix} \begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{bmatrix} \begin{bmatrix} x\\ y\\ 1\\ \end{bmatrix}\]Burada $(x’,y’)$ çiftlerinin $(x,y)$ çiftlerinin $a$ matrisi ile dönüşüm sonrası aldığı değerler olduğunu hatırlayalım. Amacımızın $a$ matrisini bulmak olduğunu tekrarlayarak işlemlerimize başlayalım. İlk olarak $z$ değerini $z=a_{31}x+a_{32}y+a_{33}$ şeklinde yazarak $x’$ ve $y’$ değerlerini açık şekilde yazmaya çalışalım.
\[x'=\frac{a_{11}x+a_{12}y+a_{13}}{a_{31}x+a_{32}y+a_{33}}; y'=\frac{a_{21}x+a_{22}y+a_{23}}{a_{31}x+a_{32}y+a_{33}}\]Şimdi içler dışlar çarpımı yaparak ifadeleri düzenleyelim ve kolaylık olması adına $a_{33}=1$ alalım.
\(a_{31}xx' + a_{32}yx' + x' = a_{11}x+a_{12}y+a_{13}\)ve \(a_{31}xy' + a_{32}yy' + y' = a_{21}x+a_{22}y+a_{23}\)
Elde edilen ifadeyi solda $x’,y’$; sağda ise $a’$ lü terimler olacak şekilde düzenlersek;
\(x' = a_{11}x+a_{12}y+a_{13} - a_{31}xx' - a_{32}yx'\)ve \(y' = a_{21}x+a_{22}y+a_{23} - a_{31}xy' -a_{32}yy'\)
elde edilir.
Bu denklemleri matris formunda yazacak olursak ($B = A\times a$);
\[\begin{bmatrix} x'\\ y' \end{bmatrix}= \begin{bmatrix} x & y & 1 & 0 & 0 & 0 & -xx' & -yx'\\ &&&&&&&\\ 0 & 0 & 0 & x & y & 1 & -xy' & -yy' \end{bmatrix} \begin{bmatrix} a_{11}\\ a_{12}\\ a_{13}\\ a_{21}\\ a_{22}\\ a_{23}\\ a_{31}\\ a_{32}\\ a_{33}\\ \end{bmatrix}\]ifadesi elde edilir. Burada aranılan $a$ vektörü $a = (A^{-1})B = B/A$ matris bölme işlemi ile kolaylıkla bulunabilir. Burada dikkat edilmesi gereken bir nokta elimizde sekiz bilinmeyen ($a$ vektörünün elemanları) olamasına rağmen görünürde sadece iki denklemimiz olmasıdır. Sekiz bilinmeyenli bir denklemin tek çözümünün olması için bağımsız sekiz denklem gerektiğinden bizimde çalışmada tek bir $(x,y)$ noktası yerine dört tane $(x,y)$ noktası üzerinden dönüşüm yapılarak $a$ matrisi bulunmuştur.
Şimdi gelelim kodlama kısmına. Bir önceki yazıda matris tersini bulma kısmından bahsettiğim için yapmamız gerek tek işlem A ve B matrislerini hazırlamak.
float dst_data[] =
{
dst[0].x, dst[0].y, 1, 0, 0, 0, -src[0].x * dst[0].x, -src[0].x * dst[0].y,
0, 0, 0, dst[0].x, dst[0].y, 1, -src[0].y * dst[0].x, -src[0].y * dst[0].y,
dst[1].x, dst[1].y, 1, 0, 0, 0, -src[1].x * dst[1].x, -src[1].x * dst[1].y,
0, 0, 0, dst[1].x, dst[1].y, 1, -src[1].y * dst[1].x, -src[1].y * dst[1].y,
dst[2].x, dst[2].y, 1, 0, 0, 0, -src[2].x * dst[2].x, -src[2].x * dst[2].y,
0, 0, 0, dst[2].x, dst[2].y, 1, -src[2].y * dst[2].x, -src[2].y * dst[2].y,
dst[3].x, dst[3].y, 1, 0, 0, 0, -src[3].x * dst[3].x, -src[3].x * dst[3].y,
0, 0, 0, dst[3].x, dst[3].y, 1, -src[3].y * dst[3].x, -src[3].y * dst[3].y,
};
float b_data[] = {src[0].x, src[0].y, src[1].x, src[1].y, src[2].x, src[2].y, src[3].x, src[3].y};
matrix_t *inA = matrix_create(float, 8, 8, 1, dst_data);
matrix_t *inB = matrix_create(float, 8, 1, 1, b_data);
Matrislerimizi oluşturduktan sonra katsayıları bulmak için önceki yazımızda kullandığımız matris_divide fonksiyonunu kullanacağız, ardından oluşan $8$ satırlık vektörü kullanarak $3\times 3$ lük a matrisimizi yeniden oluşturacağız.
matrix_t *inv = matrix_create(float);
matrix_divide(inA, inB, inv);
Bu aşamada istediğimiz noktaları istediğimiz yeni noktalara dönüştürecek dönüşüm matrisini elde etmiş bulunuyoruz. Elde edilen bu sonuç imlab kütüphanesinde yer alan pts2tform fonksiyonu ile de gerçeklenebilir.
Bulunan değerler kullanılarak istenilen dönüşüm imrotate fonksiyonunu ile gerçekleştirilebilir. Her zamanki gibi bir örnek uygulama ile yazımızı bitirelim. Birkaç yazı önce temelini attığımız sudoku çözücü uygulamamız için bulunan sudoku karesini hizalamaya çalışalım.
// read the test image
matrix_t *test = imread("../data/sudoku.bmp");
matrix_t *test_aligned = matrix_create(uint8_t, rows(test), cols(test), 3);
// find the key points
struct point_t source[4] = { {.x = 117, .y = 66}, {.x = 464, .y = 70}, {.x = 502, .y = 375}, {.x = 33, .y = 350} };
struct point_t destination[4] = { {.x = 0, .y = 0}, {.x = 511, .y = 0}, {.x = 511, .y = 511}, {.x = 0, .y = 511} };
// correct the image
matrix_t *transform = pts2tform(source, destination, 4);
// print the transform
printf("%5.3f %5.3f %5.3f\n", atf(transform, 0,0), atf(transform, 0,1), atf(transform, 0,2));
printf("%5.3f %5.3f %5.3f\n", atf(transform, 1,0), atf(transform, 1,1), atf(transform, 1,2));
printf("%5.3f %5.3f %5.3f\n", atf(transform, 2,0), atf(transform, 2,1), atf(transform, 2,2));
// do the transform
imtransform(test, transform, test_aligned);
// write the resulting image
imwrite(test_aligned, "../data/test_aligned.bmp");
Yazılan kod okunan sudoku resminin dört köşesini girdi olarak aldıktan sonra sudoku karesini $512 \times 512$ lik bir karenin içerisine hizalayacak dönüşüm matrisini bulur ve dönüşümü gerçekleştirir. Kodumuzun girdi ve çıktıları şu şekilde olacaktır.
| Girdi İmgesi | Hizalama İçin Seçilen Noktalar | Hizalanmış İmge |
|---|---|---|
 |
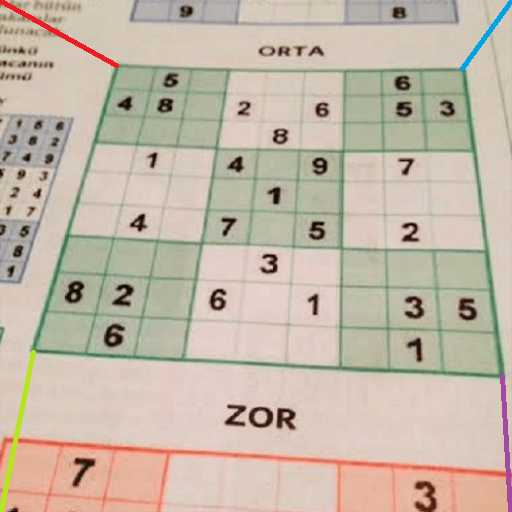 |
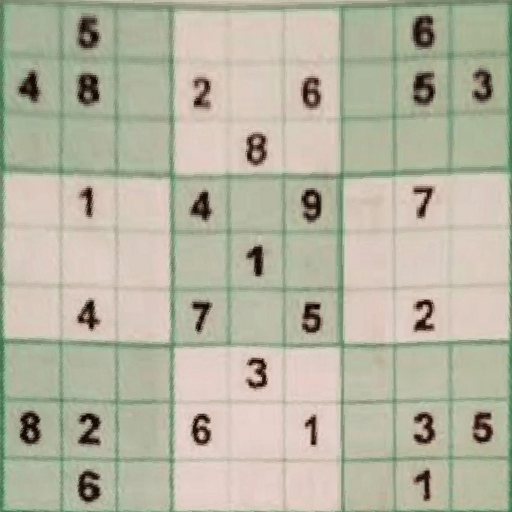 |
Başka bir uygulama olarak da rubik küp örneğine bakalım. Burada amacımız verilen rubik küpe yukarıdan baksaydık nasıl bir görüntü elde ederdik sorusuna cevap bulmak.
| Girdi İmgesi | Hizalama İçin Seçilen Noktalar | Hizalanmış İmge |
|---|---|---|
 |
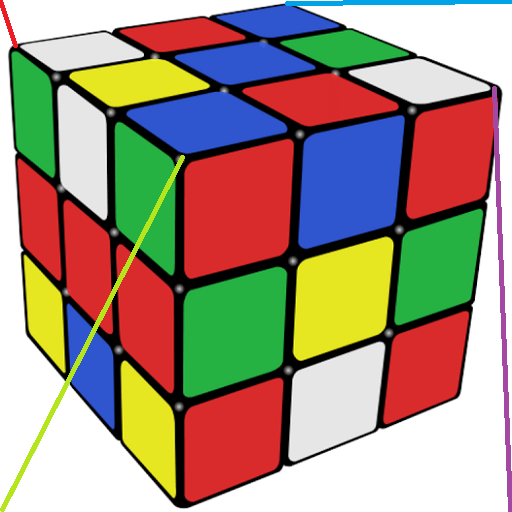 |
 |
Görüldüğü gibi algoritma sadece köşe noktalarını alarak otomatik ürettiği parametreler ile gayet başarılı sonuçlar üretmektedir. Bu da bize kamera açısından bağımsız görüntü işleme uygulamalarında büyük bir katkı sağlamaktadır.
Yazıda yer alan analizlerin yapıldığı kod parçaları, görseller ve kullanılan veri setlerine perspective_transform GitHub sayfası üzerinden erişilebilirsiniz.
Referanslar
